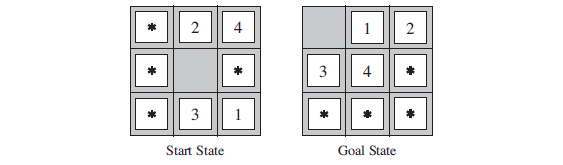
Figure 3.2
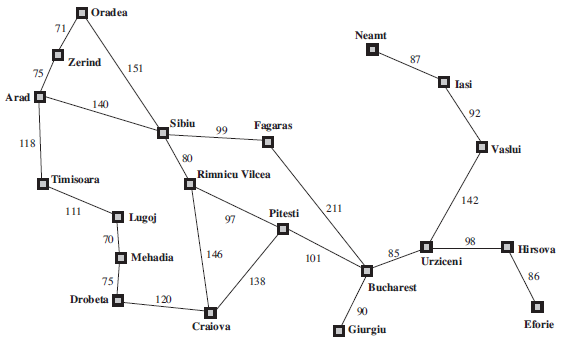
Figure 3.3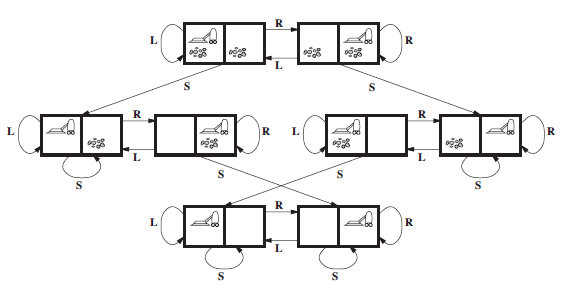
Figure 3.4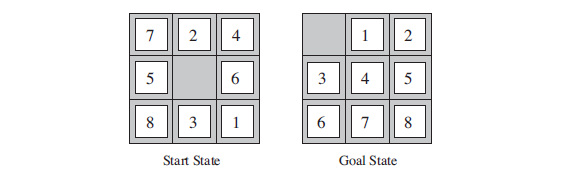
Figure 3.5
Figure 3.6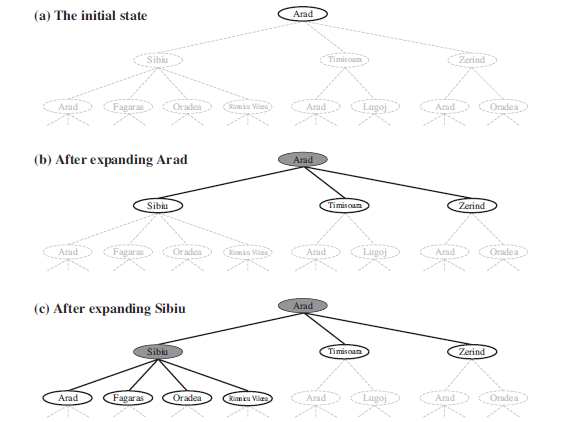
Figure 3.10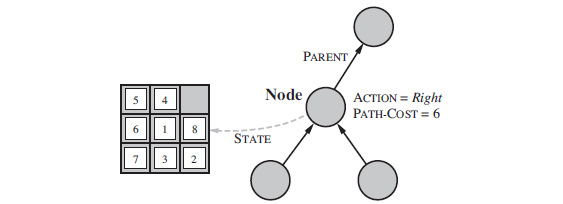
Figure 3.12
| 深さ | ノード数 | 時間 | メモリ |
|---|---|---|---|
| 2 | \(110\) | .11 ミリ秒 | 107 キロバイト |
| 4 | \(11,110\) | 11 ミリ秒 | 10.6 メガバイト |
| 6 | \(10^6\) | 1.1 秒 | 1 ギガバイト |
| 8 | \(10^8\) | 2 分 | 103 ギガバイト |
| 10 | \(10^{10}\) | 3 時間 | 10 テラバイト |
| 12 | \(10^{12}\) | 13 日 | 1 ペタバイト |
| 14 | \(10^{14}\) | 3.5 年 | 99 ペタバイト |
| 16 | \(10^{16}\) | 350 年 | 10 エクサバイト |
Figure 3.15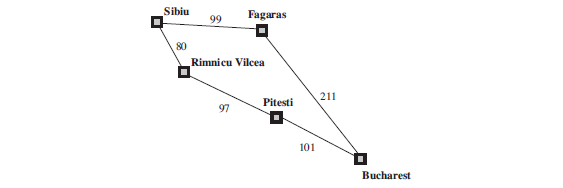
Figure 3.16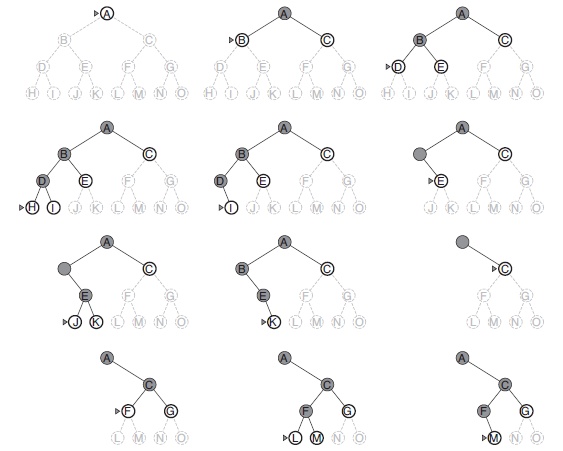
Figure 3.19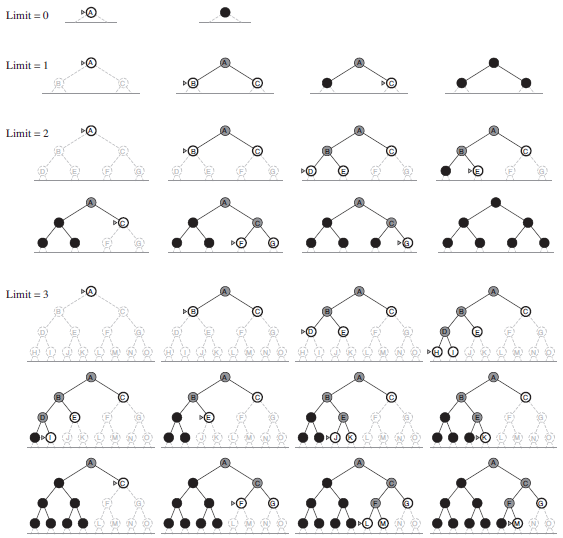
Figure 3.20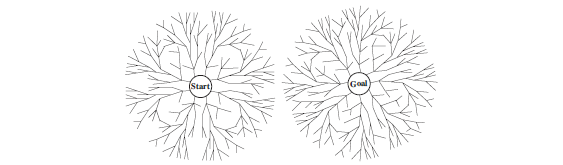
| 完全性 | 時間的複雑性 | 空間的複雑性 | 最適性 | |
|---|---|---|---|---|
| 幅優先探索 | あり ※1 | \({\mathcal O}(b^d)\) | \({\mathcal O}(b^d)\) | あり ※3 |
| 統一コスト探索 | あり ※1 ※2 | \({\mathcal O}(b^{1 + [C^* / ε]})\) | \({\mathcal O}(b^{1 + [C^* / ε]})\) | あり |
| 深さ優先探索 | なし | \({\mathcal O}(b^m)\) | \({\mathcal O}(bm)\) | なし |
| 深さ制限探索 | なし | \({\mathcal O}(b^l)\) | \({\mathcal O}(bl)\) | なし |
| 反復深化深さ優先探索 | あり ※1 | \({\mathcal O}(b^d)\) | \({\mathcal O}(bd)\) | あり ※3 |
| 双方向探索(適用可能であれば) | あり ※1 ※4 | \({\mathcal O}(b^{d / 2})\) | \({\mathcal O}(b^{d / 2})\) | あり ※3 ※4 |
Figure 3.22
Figure 3.23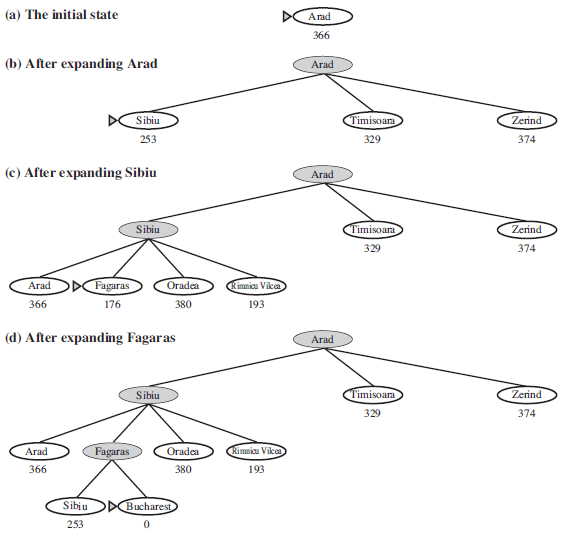
Figure 3.2
Figure 3.24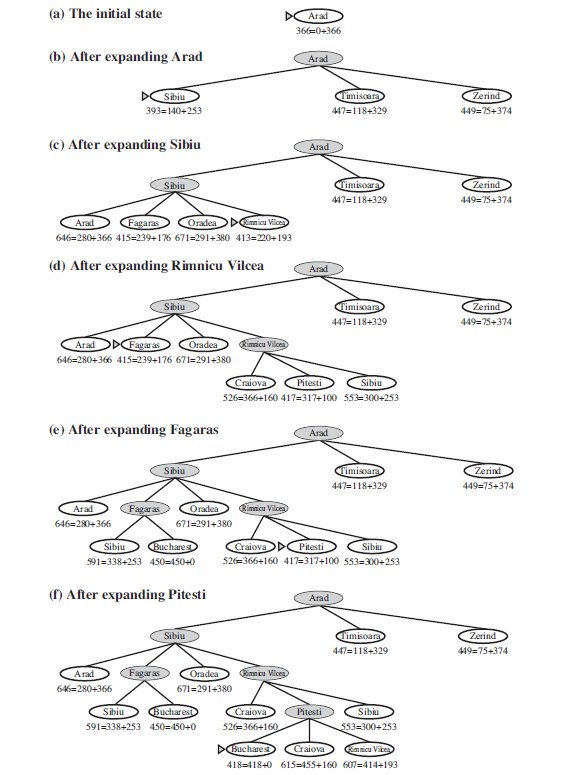
| [s1: f = 10] | ┬ | [s2: f = 20] | ─ | [s3: f = 35] |
| └ | [s4: f = 50] | ─ | [s3: f = 30] |
Figure 3.25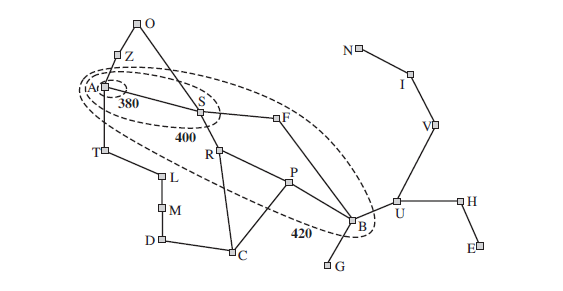
Figure 3.27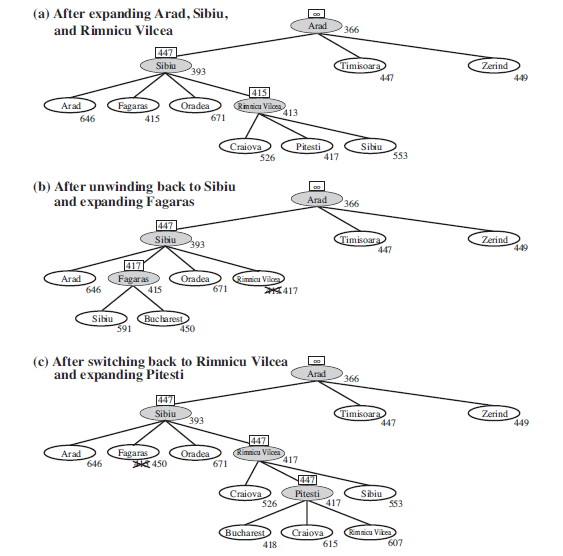
Figure 3.24
Figure 3.28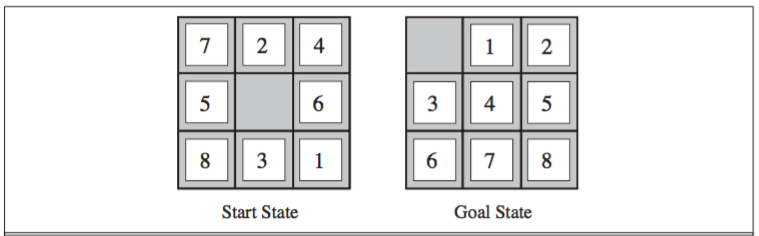
Figure 3.29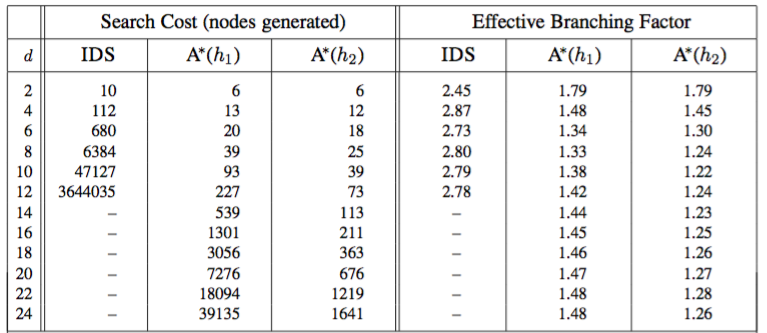
Figure 3.30